2次元フーリエ変換を用いた画像解析入門
岡部 弘高
九州大学大学院工学研究院エネルギー量子工学部門
1.はじめに
近年、画像処理や画像解析はコンピュータの発達・普及に伴って簡単、高速、安価に行うことが可能になった。衛生画像の解析、ファクシミリにおける画像圧縮、郵便番号読み取りなどのパターン認識、さらに動画の圧縮転送まで非常に広い分野で常識化している。ここでは2次元画像でよく行われているフーリエ変換を用いた周期性の評価法に関する基本的な事柄の解説を行う。
2.画像について
2.1.ディジタル画像
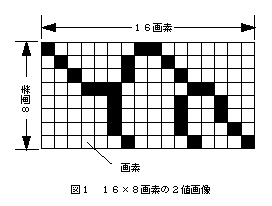 コンピュータで処理可能なディジタル画像とは画素 (Pixel) と呼ばれる点の集合である。画素は図1のように2次元格子状に配置され、(横方向の画素数)×(縦方向の画素数)画素の画像と呼ばれる。図1は 16×8 画素の画像である。画素が多いほど高解像度の画像であり、細かい表現が可能になる。
コンピュータで処理可能なディジタル画像とは画素 (Pixel) と呼ばれる点の集合である。画素は図1のように2次元格子状に配置され、(横方向の画素数)×(縦方向の画素数)画素の画像と呼ばれる。図1は 16×8 画素の画像である。画素が多いほど高解像度の画像であり、細かい表現が可能になる。
さらに各画素は明るさや色によって特徴付けられる。明るさは、最も明るい状態と真っ暗な状態を何段階で表現するかによって何階調と呼ばれる。色は、赤、緑、青の光の三原色の混合比で表す。例えば、白は赤、緑、青を1:1:1の明るさ比で混合したもののうち最も明るい色である。同じ混合比でも、明るさによって白から灰を表現することができる。三原色の明るさが0の場合が黒(暗)である。
通常用いられている全ての画像においてその画像を構成する画素が明るさと色という情報を持っているわけではなく、必要に応じて以下の3種類の画像が用いられる。
- 2値化画像:各画素が明(白)と暗(黒)の様に2つの値で表現される。
- 階調画像:各画素が何段階かの明るさを持ち、各画素の色は同じもの。白~灰~黒の場合をグレースケールと呼び一般的に用いられている。
- カラー画像:各画素が階調だけでなく、色を持つもの。通常は赤、緑、青の三原色が各々階調を持つとして表現される。
1. から 3. になるにつれて表現力(情報量)が大きくなる代わりに保存や処理に必要なコストが増大することになる。
2.2.画素の値
画素の値とは、2値化画像や階調画像ならば明るさであるが、カラー画像は色に対する情報をどのように扱うかを注意する必要がある。例えば、赤、緑、青別に処理するのか、赤、緑、青の明るさ値を加えて絶対的明るさを画素値とするのか等である。また、カラー画像には赤、緑、青の比率を表す情報と各画素が表す色の情報を別々に保持するインデックス方式もある。例えば、最も普及している Windows95 のグラフィック画面には 1600万色の中から任意の 256 色を表示するモードがある。各画素に対応する情報は 1600万色中の何番目の色かを保持している(0~256の数字、即ちインデックスである)。一方、何番目の番号がどのような色かは赤、緑、青の各明るさが256段階(256 × 256 × 256 で 1600万色)で表される。画面に表示されるときには、インデックスと色情報はハードウェアで対応させられる。この様な方式の違いによって、画像の読み込みと処理を異なるソフトウェアで行う場合には画像形式の変換が必要になることがある。
3.画像の取扱い
3.1.画像の読み込み
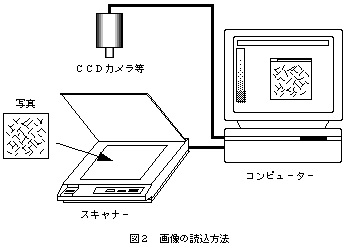 画像をコンピュータで処理したい場合には、画像をディジタル化しておく必要がある。普通の写真対象物であれば、最も簡単なのは、対象物をCCDカメラ等によって直接撮影し、その画像を接続したコンピュータに読み込む方法であろう。しかし、それが出来ない場合にも写真を撮ることができれば、写真をスキャナーで読み取ることによってディジタル画像化が可能である(図2参照)。
画像をコンピュータで処理したい場合には、画像をディジタル化しておく必要がある。普通の写真対象物であれば、最も簡単なのは、対象物をCCDカメラ等によって直接撮影し、その画像を接続したコンピュータに読み込む方法であろう。しかし、それが出来ない場合にも写真を撮ることができれば、写真をスキャナーで読み取ることによってディジタル画像化が可能である(図2参照)。
3.2.画像処理ソフトウェア
画像をコンピュータに読み込んだらそれを処理するソフトウェアが必要になる。自作や購入以外にも高度な機能をもったフリーソフトウェアをインターネットから得ることが出来る。例えば、様々なOS(Windows,Mac,Linux等)のJava仮想マシンで動くImageJがある。
4.周期性の評価
4.1.二次元フーリエ変換
周期性の評価に欠かせないのがフーリエ変換であり、2次元の場合も音の周波数解析(1次元)と基本は同じである。音では元データが時間の経過に伴うものであるのに対し、画像の場合には位置が変わることによるものになる。従って、フーリエ変換後の次元は元データの次元の逆数となるので、音が周波数(単位は s-1 =Hz)に変換されるのに対し、このような画像では波数(空間周波数ともいう。波長λとして、k = 1/λ、またはk = 2π/λが用いられる。;単位 m-1 )に変換される。また、フーリエ変換で扱えるのは通常グレースケールの画像なので、カラーを扱うには原色別などの工夫が必要になる。
図3(a)は横方向に正弦波的周期性で明るさが変化する画像である。図3(a)のグレースケールの画像を二次元フーリエ変換し、パワー(絶対値の自乗)を濃淡で表したのが図3(b)である。図3(b)の中心が波数0になる。中心を挟んで左右に同じだけ離れた輝点が現れている。この点が図3(a)における正弦波の周期に対応する点である。中心から輝点への方向は、正弦波の方向と一致する。1つの方向に対し、向きは2つあるので、波数0の点を中心として2つの対象な点が現れることになる。また、輝点の中心からの距離が正弦波の波数を表している。図3(b)の四隅で波数は最も大きくなり、その大きさは画素数と元データの大きさから決まる。即ち、画像が x × x 画素であり、画像の一辺の大きさを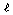 m とすると、四隅の波数の絶対値は、
m とすると、四隅の波数の絶対値は、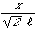 (m-1)
であり、そのときの横方向と縦方向の各成分は、
(m-1)
であり、そのときの横方向と縦方向の各成分は、
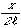 (m-1)
となる。横と縦の画素数はフーリエ変換を高速(実用に耐える早さで)に行うためには2の累乗にする必要がある。よく用いられるのは、128×128、256×256、512×512等である。また、波数の最大値は画像の一辺の大きさが同じならば画素数に比例することに注意しなければならない。例えば図3は256×256画素であるが、同じ画像が 512×512画素で構成されている場合には図3(b)の輝点はAの位置に、128×128画素ならばBの位置に現れる。
(m-1)
となる。横と縦の画素数はフーリエ変換を高速(実用に耐える早さで)に行うためには2の累乗にする必要がある。よく用いられるのは、128×128、256×256、512×512等である。また、波数の最大値は画像の一辺の大きさが同じならば画素数に比例することに注意しなければならない。例えば図3は256×256画素であるが、同じ画像が 512×512画素で構成されている場合には図3(b)の輝点はAの位置に、128×128画素ならばBの位置に現れる。
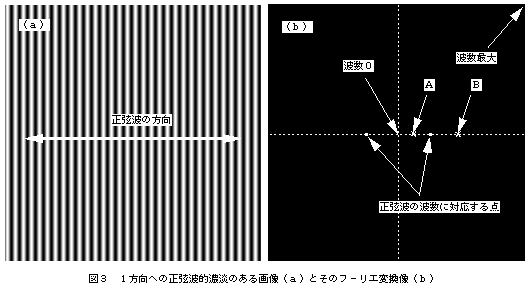
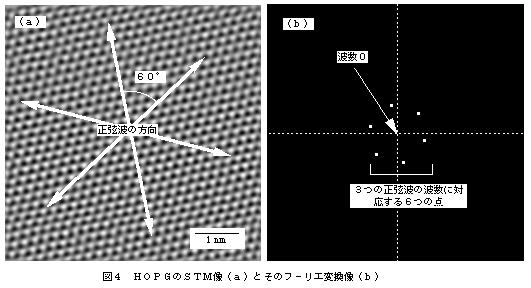
図4(a)はHOPG(高配向焼結グラファイト)のSTM(走査型トンネル顕微鏡)像である。STM像は電子の密度分布を反映したものであり、HOPGでは60度づつ方向の異なった3つの正弦波の重なったもので近似できることが知られている。フーリエ変換像(図4(b))では3つの正弦波に対応する6つの点が現れており、各点は波数0の点を中心に60度づつ回転した位置にある。
4.2.解析例(薄膜電子顕微鏡像の周期性評価)
図5(a)はHOPG基板上のパラフィン蒸着膜の透過型電子顕微鏡像である。この蒸着膜はHOPG基板にエピタキシャル成長していると考えられている。図5(a)のα、β、γの方向には周期的構造がみられる。その周期は矢印で示したように長いものから短いのまで様々である。この周期に対応する波数が図5(b)のフーリエ変換像では色の濃い部分として表れている。すなわち、α、β、γの方向の様々な波数に対応するα、β、γ方向の画素が濃く表れている。
一方、周期性を示していても、それは他の方向の周期性の射影という場合がある。例えば図5(a)から分かるように、δ方向も周期性を示しているが、蒸着膜のパターンの方向とは直交しておらず、図5(b)ではδ方向は濃くなっていない。すなわち、δ方向の周期性はα、β、γ方向の周期性の射影であることがフーリエ変換像では明らかとなるのである。図5(b)のようにHOPG基板上のパラフィン蒸着膜は図4(b)で示したHOPGと同じ対称性を示し、エピタキシャル成長したことの有力な証拠となっている。

一方、HOPGのような周期構造を持たないガラス基板上のパラフィン蒸着膜(図6(a))ではパターンの大きさにはさほど違いはない(倍率が違うことに注意)が、フーリエ変換した画像(図6(b))は特徴のないハローパターンになるだけで明らかな対称性は示さない。また、図5(b)、6(b)の円はパターンの幅(約 0.6 μm)の波数に対応しており、その外で色が薄くなるのは、これ以上小さい構造は少ないことを示している。

もちろん、以上のような解析を顕微鏡写真自体から行うこともある程度は可能であろう。しかし、フーリヘ変換による波数解析を行うことによってより定量的な取り扱いが可能になるのである。
5.おわりに
以上、2次元フーリエ変換を用いた周期性の評価について簡単に解説した。一般に、画像処理はその限界をわきまえなければ誤った結論を導くことにもなりかねない。ソフトウェアを自作しない人でも処理の内容をある程度理解しておくことが大切である。また、ここでは写真画像を念頭において説明したが、2次元の分布として画像の様に表現されたものであれば、次元(単位)が変わるだけで周期性の評価は同様に行うことは容易であろう。
参考文献
画像処理の一般的解説書は以下の文献以外にも多数出版されているので目的に応じて選ぶとよいだろう。
- 牧島邦夫、篠原靖忠、小森尚志訳「計量形態学」内田老鶴圃刊
- 木内雄二著「画像認識のはなし」日刊工業新聞社刊
- 安居院猛、中嶋正之、木見尻秀子著「C言語による画像処理」昭晃堂刊
- 丹慶勝市、奥村晴彦、佐藤俊郎、小林 誠訳「NUMERICAL RECIPES in C [日本語版]」技術評論社刊
- 顕微鏡画像の波数解析、岡部弘高、石田謙司、瀧 正二、原 一広、九大中央分析センタ-ニュ-ス11 (1994) 4
本文は岡部が参考文献5を一部内容を変更・更新して1998年頃にHTML用に書き改め公開したものです。アクセスが公開以来  と多いので残し、少し改訂していますが、コンピュータ環境などに少し古い記述が残っています。
と多いので残し、少し改訂していますが、コンピュータ環境などに少し古い記述が残っています。
 コンピュータで処理可能なディジタル画像とは画素 (Pixel) と呼ばれる点の集合である。画素は図1のように2次元格子状に配置され、(横方向の画素数)×(縦方向の画素数)画素の画像と呼ばれる。図1は 16×8 画素の画像である。画素が多いほど高解像度の画像であり、細かい表現が可能になる。
コンピュータで処理可能なディジタル画像とは画素 (Pixel) と呼ばれる点の集合である。画素は図1のように2次元格子状に配置され、(横方向の画素数)×(縦方向の画素数)画素の画像と呼ばれる。図1は 16×8 画素の画像である。画素が多いほど高解像度の画像であり、細かい表現が可能になる。 画像をコンピュータで処理したい場合には、画像をディジタル化しておく必要がある。普通の写真対象物であれば、最も簡単なのは、対象物をCCDカメラ等によって直接撮影し、その画像を接続したコンピュータに読み込む方法であろう。しかし、それが出来ない場合にも写真を撮ることができれば、写真をスキャナーで読み取ることによってディジタル画像化が可能である(図2参照)。
画像をコンピュータで処理したい場合には、画像をディジタル化しておく必要がある。普通の写真対象物であれば、最も簡単なのは、対象物をCCDカメラ等によって直接撮影し、その画像を接続したコンピュータに読み込む方法であろう。しかし、それが出来ない場合にも写真を撮ることができれば、写真をスキャナーで読み取ることによってディジタル画像化が可能である(図2参照)。
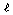 m とすると、四隅の波数の絶対値は、
m とすると、四隅の波数の絶対値は、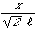 (m-1)
であり、そのときの横方向と縦方向の各成分は、
(m-1)
であり、そのときの横方向と縦方向の各成分は、
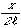 (m-1)
となる。横と縦の画素数はフーリエ変換を高速(実用に耐える早さで)に行うためには2の累乗にする必要がある。よく用いられるのは、128×128、256×256、512×512等である。また、波数の最大値は画像の一辺の大きさが同じならば画素数に比例することに注意しなければならない。例えば図3は256×256画素であるが、同じ画像が 512×512画素で構成されている場合には図3(b)の輝点はAの位置に、128×128画素ならばBの位置に現れる。
(m-1)
となる。横と縦の画素数はフーリエ変換を高速(実用に耐える早さで)に行うためには2の累乗にする必要がある。よく用いられるのは、128×128、256×256、512×512等である。また、波数の最大値は画像の一辺の大きさが同じならば画素数に比例することに注意しなければならない。例えば図3は256×256画素であるが、同じ画像が 512×512画素で構成されている場合には図3(b)の輝点はAの位置に、128×128画素ならばBの位置に現れる。


